고정 헤더 영역
상세 컨텐츠
본문
우리는 회귀분석에서 횡단면 자료를 분석하였고 시계열에선 시계열자료를 분석하였다.
그럼 패널 데이터란 무엇일까? 패널 데이터는 횡단면 자료와 시계열 자료의 성격을 섞어둔것이다
정확히 말하자면 고정된 대상을 시계열로 관찰한 것이다
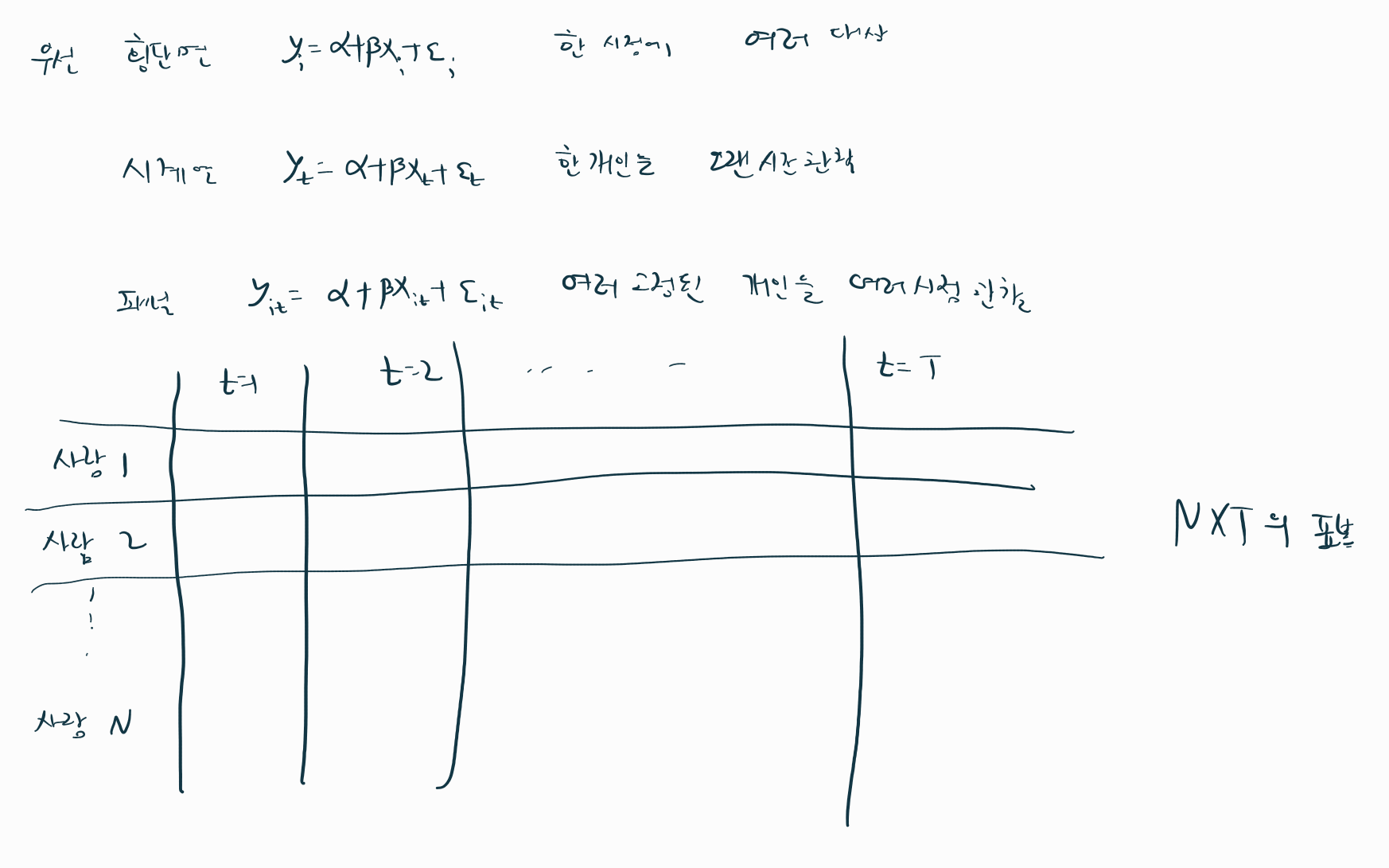
그렇다면 패널데이터를 이용해서 회귀분석은 어떻게 할 수 있을까?
크게 pooled ols라고 불리는 합동 ols 방식 FE라고 불리는 고정효과 방식 RE라고 불리는 랜덤효과방식이 있따.
일단 패널데이터의 성격을 알아볼 필요가 있다.

횡단면 자료와 시계열 자료의 결합 형태다 보니 횡단면의 오차항과 시점에 따른 오차항이 존재한다.
즉 필연적으로 자기상관이 생길수밖에 없으며 U의 존재로 인해 내생성의 문제가 나타날 가능성이 높다.
사실 자기상관은 효율성의 문제일 뿐 불편,일치추정량을 구하는데는 문제가 없다.
하지만 내생성은 다르다. 올바른 추정량을 구할 수 없다.
즉 우리는 1번 합동 OLS 방식은 잠시 내려두어야 한다. (자기상관과 내생성 문제)

먼저 2번의 고정효과 방식은 각 대상의 Ui 항 즉, 횡단면의 오차항을 절편으로 고정시키는 방식이다.
절편이 몇번째 대상인지에 영향을 받는다는 것이다.
대표적으로 LSDV라는 방식을 사용한다. 더미변수를 이용하는 것이다.
우리가 합동OLS 방식 대신 LSDV를 사용하는 이유는 무엇이었나면 내생성 문제를 일으키는 U를 오차항에서 제거하기 위함이었다.
하지만 만약 더미변수들의 회귀계수가 0이라는 것은 애초에 U라는 것이 존재하지 않았다는 뜻이다.

즉, 더미변수들의 회귀계수가 전부 0이라면 굳이 LSDV 방식을 사용할 필요가 없다.
하지만 이 가설이 기각되어버린다면 LSDV를 사용하는게 좋을것이다.
FE 고정효과 방식은 LSDV만이 있는 것이 아니다.
FD,LD,WG 등 다양하게 U를 제거하는 방식을 사용한다 .
대표적으로 WG를 알아보겠다.

U를 제거하는 방식을 위와 같이 보였다. U는 시간에 영향받지 않고 일정하다는 점에서 시계열 관점에서 평균과 그 값이 동일할 것이다. 그렇기에 차분을 통해 제거할 수 있다.
이제 확률효과 모형을 살펴보겠다.
애초에 U는 존재하지만 U에 내생성이 없다면? 이라는 가정 하에서 실행하는 것이 확률효과 모형이다.

차이를 잘 알 필요가 있다.

이렇게 내생성이 없는 상황이라면 자기상관을 해결하는 GLS 방식을 통해 추정한다면 더 효율적인 추정량을 구할 수 있을 것이다.
결론적으로 고정효과와 랜덤효과는 내생성이 있냐 없냐의 차이이다.
당연하게도 내생성이 없다면 랜덤효과추정량이 더 좋을 것이다.
그렇다면 내생성 검정이 필요하다.
앞서 우리는 도구변수에서 하우스만 검정을 통해 내생성을 검정한 적이 있다. 똑같다

'계량경제학' 카테고리의 다른 글
| 로짓-프로빗 모형 (0) | 2025.02.08 |
|---|---|
| 공적분과 오차수정모형 (1) | 2025.02.07 |
| 벡터 자기회귀 모형 (VAR,SVAR) (0) | 2025.02.07 |
| 가성회귀와 ADF 검정 (0) | 2025.02.07 |
| 단위근과 DF분포 (Dickey-Fuller) (0) | 2025.02.04 |




